Game Path Planning by Julian Ceipek

Why should I care?

Path planning is a key part of the Artificial Intelligence (AI) in games. It's how units move to where you click in Starcraft. It's how enemies in Mass Effect run around cover to get to you. It's the magic that makes computer-controlled characters move towards goals efficiently while avoiding obstacles and hazards.

Getting started with proper pathfinding behavior can be daunting. The internet is filled with descriptions of the classic "A* algorithm" for grid-based navigation. But modern 3d games often involve complex environments, right? How do programmers make characters move around in those? Why don't characters zig-zag their way towards you in games with good AI?

In this tutorial, we'll take a look at making characters navigate the world using Navigation Meshes, which are used in lots of the best games available today. That technology is part of what Valve and Unreal use in their game engines.

Subdividing Space

The first part of any pathfinding AI is figuring out how to represent the game world in a way that is useful for navigation. Some of the most common representations are

Waypoints
Grids
Navigation Meshes

Everything is a Graph

The most important thing to realize about all of these representations is that they are just graphs. The first thing you thought of when I said "graph" was probably a bar or line graph.

That's not what I mean here. In game AI (and in mathematics), graphs are a series of nodes connected by edges. The simplest way to think of these terms in the context of pathfinding AI is that each node in a graph represents a possible place a character could be and each edge indicates that it is possible for the character to move between the nodes it connects. Each edge has an associated cost, which represents the effort it takes for a character to move from one node to the next. When we talk about pathfinding, we're really talking about finding a path between two nodes in a graph, ideally minimizing the cost of the path.

This is a node. It represents a place a character can be.

Characters can only move between nodes via edges.

Note: The edges we'll be looking at are bi-directional; characters can walk between them at will. More complicated edges might be one way only. For example, a character might jump down from a platform but be unable to jump back up. Don't worry, though, if you ever run into that kind of situation, the techniques we'll talk about can be applied just as easily.

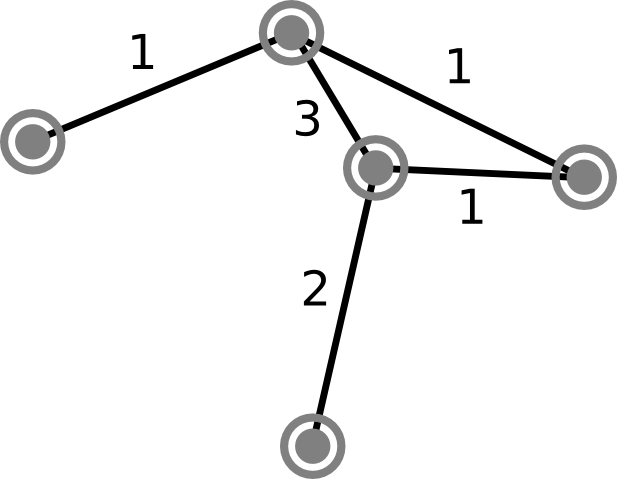
A graph is a network of nodes. Moving between nodes is costly.

The cheapest path from A to B takes 3 steps and has a total cost of 4 = 2 + 1 + 1.

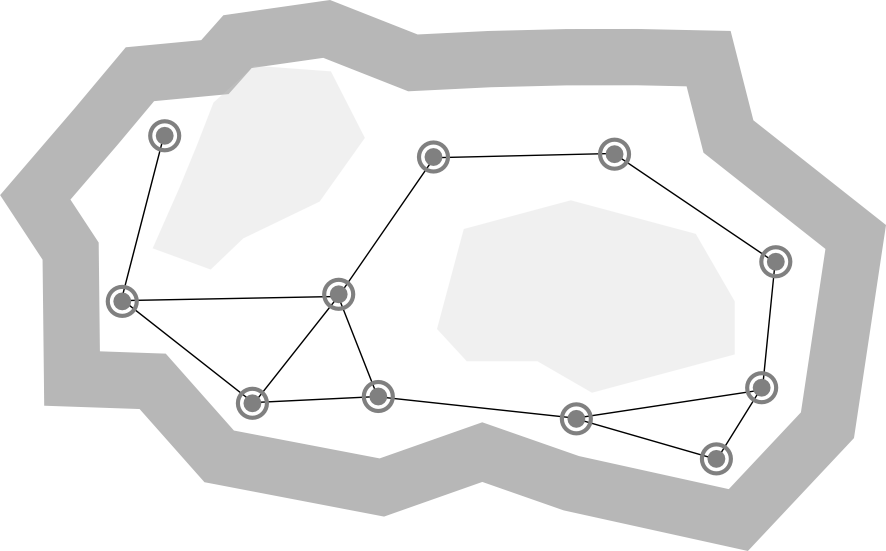
Waypoints

Waypoint representations of space are easy to create and think about, but they are not very good for pathfinding. Although they use very little memory, they result in inefficient, unrealistic paths.

The main idea behind waypoint systems is to place a small number of nodes and edges in the game world so that characters can find their way around static obstacles. Unfortunately, if characters always stay on paths between waypoints, their behavior will be unrealistically constrained. However, if they leave the waypoint network, they can get stuck easily.

A rough island world.

Waypoints around an island. Each waypoint corresponds directly to a node. The costs would just be the length of the connections between waypoints. Note that some regions are unreachable.

Grids

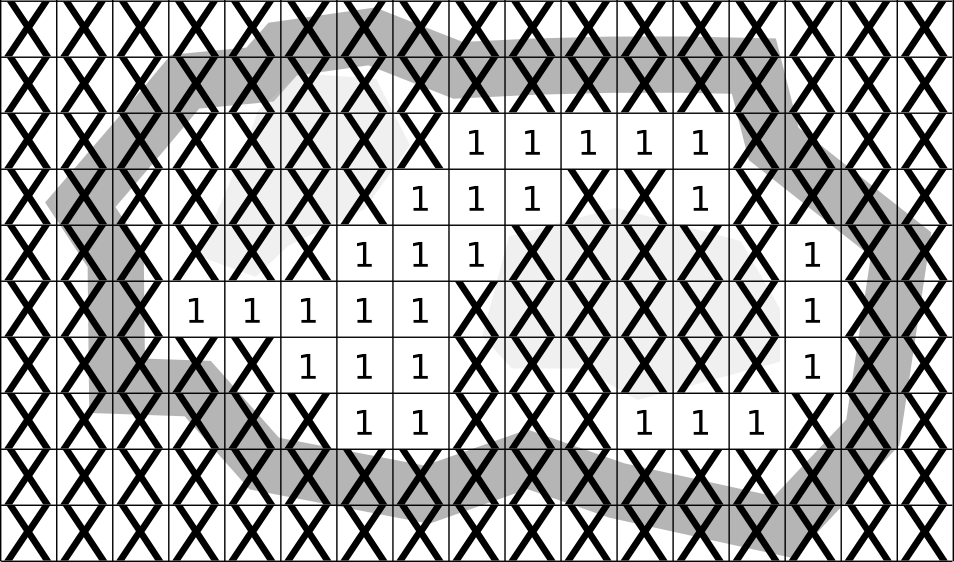
If you look for an intruductory tutorial on path planning, chances are you'll find one that uses a grid. Grids work really well for small environments, especially for games in which characters move on a grid already. More complex environments require finer grids, which can take up an infeasible amount of memory for large worlds.

You might have seen a representation of a grid like this:

The numbers in each grid square represent the difficulty or "cost" of going to that square from an adjacent square. The rough grid makes many areas unreachable. A higher resolution grid would use more memory but would represent the world more effectively.

What you might not have realized is that a grid like this is just a more compact way to represent a very dense graph:

A grid is just a graph!

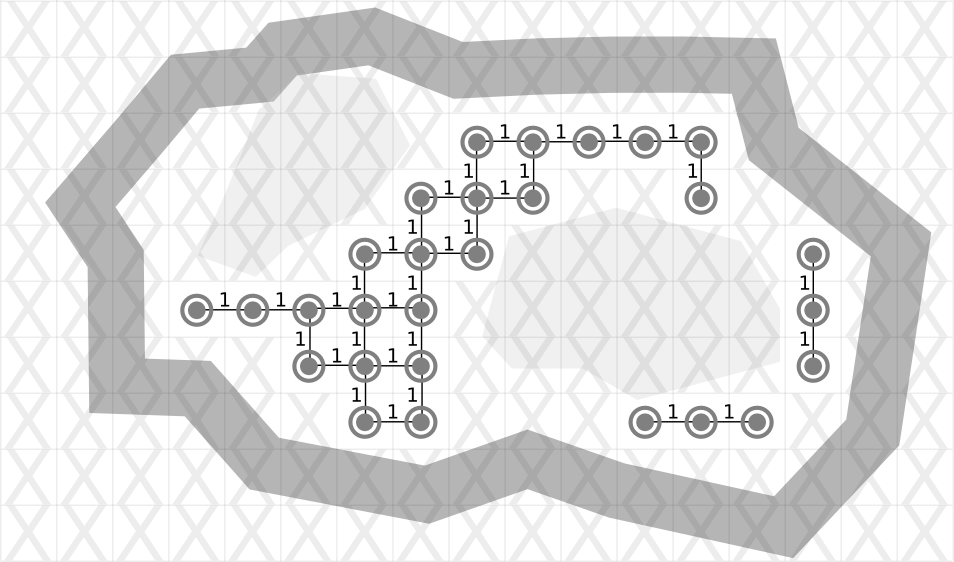
Grids don't seem to be used much for large, modern games. However, cutting-edge AI researchers are finding uses for them for very localized navigation in conjunction with other techniques such as navigation meshes.

Navigation meshes are an efficient way to represent walkable regions in a game world. A common implementation relies on connected convex polygons.

Navigation meshes efficiently describe walkable regions in the world.

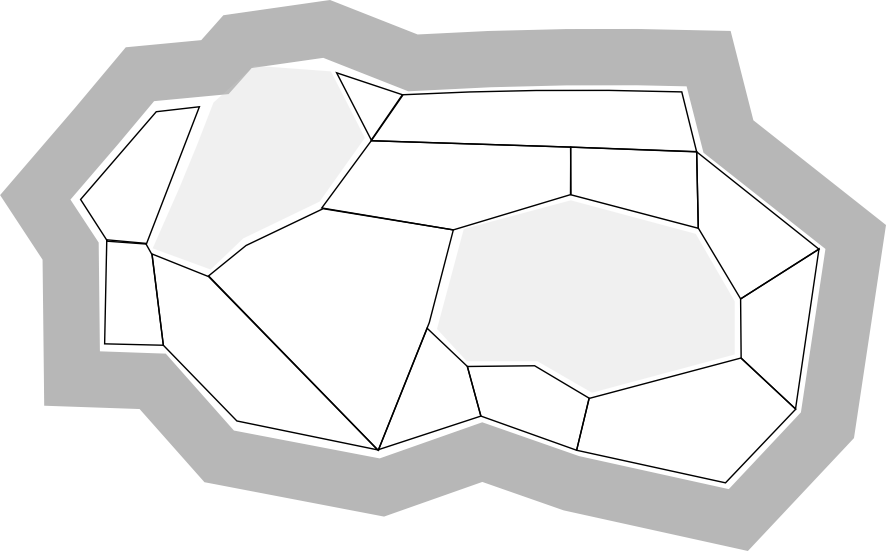
Just like in the grid representation, each polygon is a node and each edge shared by two polygons represents a connection between nodes.

A Navigation Mesh is also just a graph!

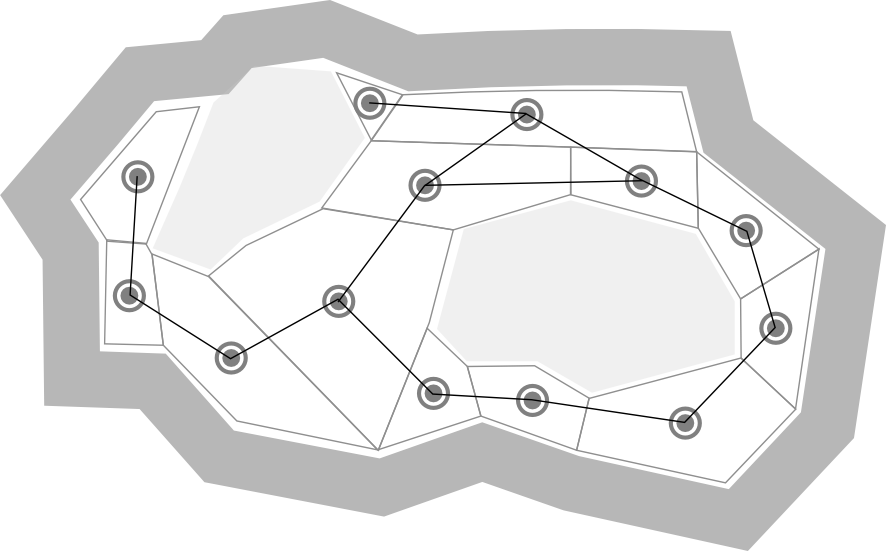
Finding Paths with A*

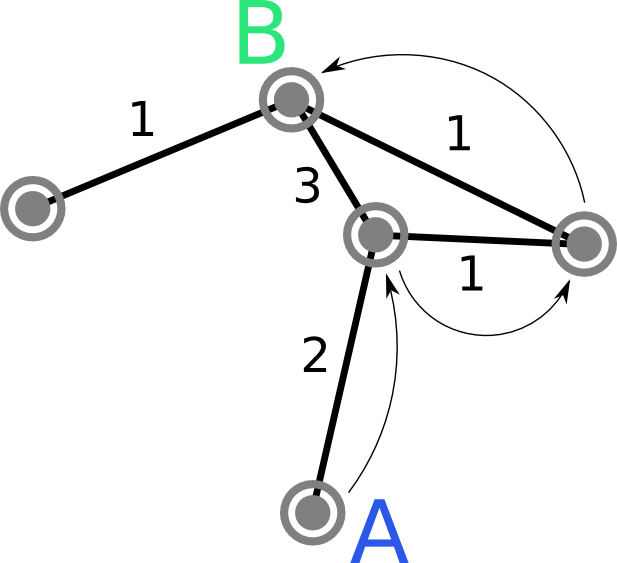
Great! We can represent space: now what? How will that help our characters get where we want them to go? The answer is: search. The A* (pronounced "A-star") algorithm is an efficient way of finding the cheapest path between two points on a graph.

There are many great explanations available online, so I won't go into a lot of detail, but the main idea behind A* is to maintain a frontier of unexplored nodes a character could visit at any point in time and to explore the one most likely to be part of the least costly path to the goal first. To do this, it uses a heuristic function that estimates the cost from a node to the goal. The simplest type of heuristic that works for A* simply returns the distance between the node and the goal. Here's an example A* implementation:

// Returns a list representing the optimal path between startNode and endNode or null if such a path does not exist // If the path exists, the order is such that elements can be popped off the path // Note: if you use this code in Javascript, make sure that the toString function of each node returns a unique value FindRoute = function (startNode, goalNode) { var frontier = PriorityQueue({low: true}); // Priority Queue (https://github.com/STRd6/PriorityQueue.js), // what have we not explored? var explored = new Set(); // Set (https://github.com/jau/SetJS), what have we explored? var pathTo = {}; // A dictionary mapping from nodes to nodes, // used to keep track of the path // The node that is the key var gCost = {}; // A dictionary mapping from nodes to floats, // used to keep track of the "G cost" associated with traveling to each node from startNode pathTo[startNode] = null; gCost[startNode] = 0.0; frontier.push(startNode, 0.0 + HeuristicCostEstimate(startNode, goalNode)); while (!frontier.empty()) { // While the frontier remains unexplored var leafNode = frontier.Values[0]; if (leafNode == goalNode) { // We found the solution! Reconstruct it. var path = []; var pointer = goalNode; while (pointer != null) { path.push(pointer); pointer = pathTo[pointer]; } return path; } frontier.pop(); explored.add(leafNode); for (var i = 0; i < leafNode.linkedTo.length; i++) { var connectedNode = leafNode.linkedTo[i]; if (!explored.contains(connectedNode) && !frontier.includes(connectedNode)) { gCost[connectedNode] = gCost[leafNode] + CostBetween(leafNode, connectedNode); pathTo[connectedNode] = leafNode; frontier.push(connectedNode, gCost[connectedNode] + HeuristicCostEstimate(connectedNode, goalNode)); } } } return null; // No path could be found }

The result of A* on a navigation mesh.

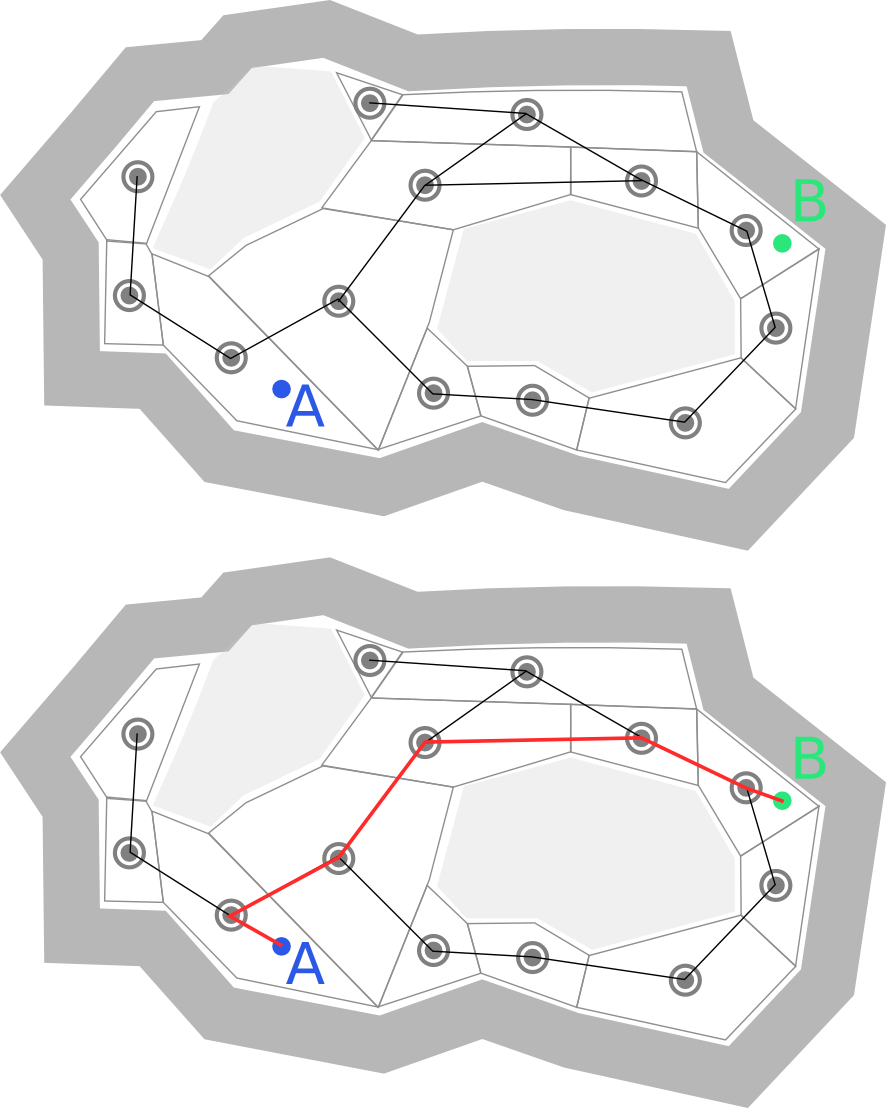
Mapping Paths to Space

Now what? We have some optimal path in an abstract graph. How does that help our characters move? The answer to that question depends a lot on the specifics of the game you're making. In some games, you can probably get away with mapping the graph directly to physical space. In most cases, though, you need to smooth the resulting path somehow. In Left 4 Dead, characters move between portal midpoints and smooth their path by moving towards a visible node that is part of the optimal A* path but is several steps ahead.

We can do better, though. If we are using a grid or navigation mesh, we can implement a smoothing technique known as the Simple Stupid Funnel Algorithm, a practical path smoothing technique developed by the lead AI programmer from the original Crysis, based on a PHD thesis on pathfinding.

The Simple Stupid Funnel Algorithm

This algorithm is all about smoothing paths by finding corners on the minimum distance path of a navigation mesh without leaving the walkable area. The result is the same as if the A* path were a string being pulled until it was taut.

The algorithm proceeds as follows:

Create a list of the portals along the A* path. Make sure that the points of each portal are stored the same way relative to the character. You will need to know if a point is to the left or right of the character.
Create a "funnel" with three points: the characters starting location (the apex), the right side of the portal, and the left side of the portal.
Alternate updating the left and right sides of the "funnel," making it narrower each time
When the sides of the funnel cross, make the point you didn't update the apex of the new funnel, and store it as part of the smoothed path.

Step-by-step demonstration of the funnel algorithm.

You can find the defacto C implementation of the funnel algorithm here. However, you'll probably have to adapt it to fit your project because it is highly implementation-dependent.

A key part of writing your own implementation depends on understanding how to tell if the funnel is crossing itself. One of the easiest and most efficient ways to do this involves the cross product. In 2d, we can use the sign of the non-zero component of the cross product to tell us the order of the points in a triangle. In most 3d game environments, we can simply disregard the third dimension for the sake of path smoothing, since most characters don't need to walk on ceilings or perfectly vertical walls.

// This function from http://digestingduck.blogspot.com/2010/03/simple-stupid-funnel-algorithm.html // is called "triarea2" because the cross product of two vectors // returns the area of the parallellogram the two sides form // (which has twice the area of the triangle they form) // The sign of the result will tell you the order of the points passed in. inline float triarea2(const float* a, const float* b, const float* c) { const float ax = b[0] - a[0]; const float ay = b[1] - a[1]; const float bx = c[0] - a[0]; const float by = c[1] - a[1]; return bx*ay - ax*by; }

Steering

We took an A* path and smoothed it, but the characters still move unnaturally! This is where steering behavior comes into play. Real people don't make point turns when they go around corners (or at least most people don't, anyway...), why should your characters? The smoothed A* path is a great guide for environment navigation, but it doesn't need to be followed exactly. One of the simplest things you can do is to implement a path following behavior that tells characters to generally stay within range of the smoothed path and to steer back towards it if they are getting off-track. You can combine multiple behaviors together to get even better results.

Resources

That's it for now! If you're interested in exploring pathfinding even further, I highly reccomend the following:

Have fun!